Research Interests

Concepts and ideas

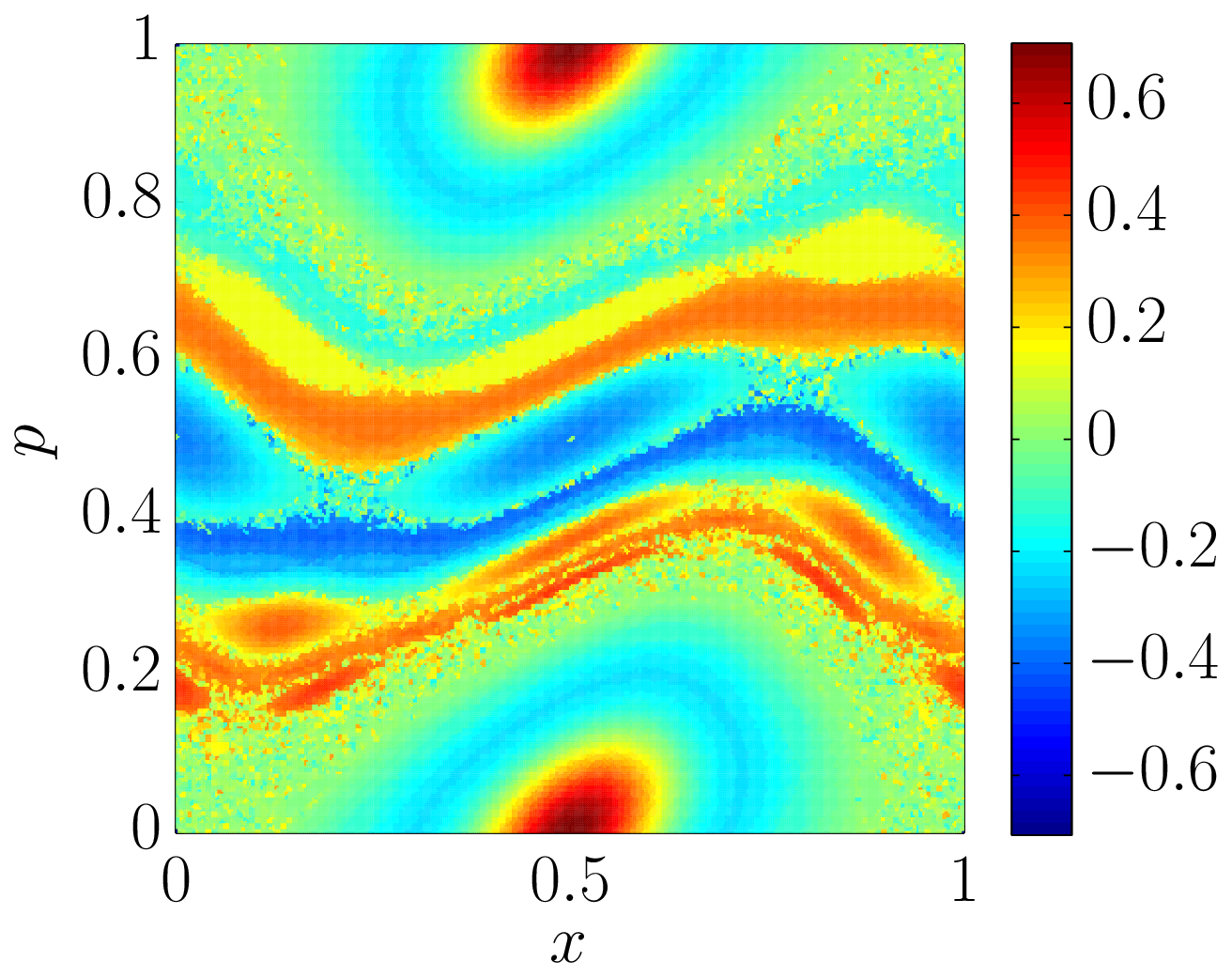Koopman operator is a representation of nonlinear dynamical system using an infinite-dimensional operator. It provides us with a “target” for approximation of nonlinear dynamics using linear operators. My interests are in characterizing three spectral objects associated to Koopman operator: 1) spectrum itself, whose discreteness/continuity relates to the amount of disorder in the dynamics, 2) eigenfunctions, whose geometry is related to geometry of invariant/periodic sets, 3) Koopman modes, that serve as “spectral analyzers” for measurements/observations. I collaborate on this topic with Igor Mezic, Mihai Putinar, Ryan Mohr, and Akshat Kumar.

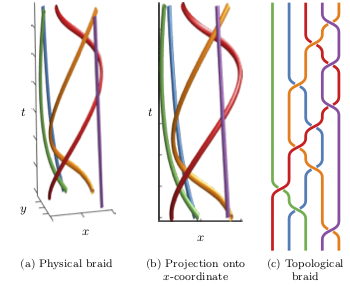Braids are mathematical structures that capture the topology of objects weaving/braiding around each other. My interests are in connecting dynamics of braids with dynamical systems from which they originate, representations of braids using piecewise-linear functions, and statistics of braids generated by stochastic processes. I am additionally actively involved in developing computational package Braidlab for working with braids (see the end of this page). On this topic I maintain collaboration with Jean-Luc Thiffeault.

Chaotic advection is a term coined by H. Aref to describe the transport of material in chaotic fluid flows, where the outcome appears similar to random agitation of fluid, but the mechanism behind this outcome is deterministic. From my earliest days in graduate school, I have worked on characterizing regions in which material moves coherently, and quantifying how much disorder there is in regions where material moves chaotically. On this topic I have, among others, worked with Igor Mezic, Stefan Siegmund, and Jean-Luc Thiffeault.

Topological and geometric inference concerns learning information about geometric objects from finite and noisy samples. My interest here stems from working with diffusion coordinates (Diffusion Maps) to understand fractal objects that represent invariant sets in dynamical systems. Presently, I am exploring both what non-diffusive motion of graphs can tell us about their geometry, and how the persistent homology can be merged with statistics and signal processing.

Applications

Unsteady aerodynamic flows are a rich source of coherent behavior (vortex shedding, shock-buffet, flutter, …) that is embedded in a turbulent flow. Such flows therefore pose an excellent testbed for merging classical nonlinear dynamics with modern machine learning tools. My current collaboration with Brian Helenbrook and Pat Piperni (Clarkson MAE), with our student Sathsara Dias, is focused on optimization of geometry of airfoils with the aid of Koopman/Dynamic Mode Decomposition.

Oceanic flows are a dynamical system that couples a wide range of spatial scales, temporal scales, and various physical components. My interest is in understanding to what degree macroscopic phenomena (tides, currents, eddies) influence the movement of water, material, or organisms in the ocean? In reference to oceanic flows, I have worked on understanding coherence in material transport (invariant sets, mesochronic analysis), quantifying disorder using braids, and using Dynamic Mode Decomposition to identify dynamically-separate components that interact in regional flows. Among my collaborators have been Igor Mezic, Jean-Luc Thiffeault, Thomas Peacock, Erik Bollt, and Michael Allshouse, and my students Aishah Albarakati, Sathsara Dias, and Toop Indoung are working on topics relating to this theme.

Coherent motion of cells occurs in various situations in the human body: cells sometimes migrate to the source of food, toward or away from pathogens, or in response to enviornmental stimuli. In this relatively-new collaboration with Shantanu Sur and Sumona Mondal, and students Alfred Worrad, Thevasha Sathiyakumar, and Morgan Reynolds, we are using persistent homology and statistical techniques to identify when a collection of cancer cells starts moving coherently based on stochastic models and experimental observations of cells.

Numerical codes and packages

Braidlab is a MATLAB toolbox that implements a large set of algorithms for manipulating braid groups, and constructing them from dynamical trajectory. Jean-Luc Thiffault, who was my postdoc supervisor, is the primary author of the package, while I remain an active developer. The package is freely available from http://github.com/jeanluct/braidlab.

ContinuousFlows is a MATLAB package that provides a common framework for simulating and analyzing dynamical systems defined by Ordinary Differential Equations. It arose from my need to test algorithms on several different ODEs in parallel. After standardizing the simulation interface that includes, e.g., running many parallel trajectory, I have over the years added calculation of FTLEs, various visualizations and computations to the package. The package is freely available from https://github.com/mbudisic/Continuous-Flows.